在量子场论中,随着费曼图的圈数增加,物理量理论值的精度将会得到提高,但相应地精细计算难度极大增加。近期,理论物理团队在量子场论精细计算方面取得了一系列重要新进展,在多圈费曼积分的解析计算新方法的探索上取得系列创新成果,分别发表在量子场论与粒子物理领域三大著名期刊《Physical Review D》、《European Physical Journal C》与《Journal of High Energy Physics》。
1、提出费曼积分在格拉斯曼流形子簇上构建基础解系
相关工作“Feynman integrals of Grassmannians”发表在《Physical Review D》(2022, 106, 116025),冯太傅教授为第一兼通讯作者,张海斌副教授与中科院理论物理研究所张肇西院士为共同通讯作者。
该论文利用费曼积分的参数化表示,将费曼积分嵌入到格拉斯曼流形子簇上,从而得到易于求解的满足费曼积分在格拉斯曼流形子簇上的GKZ超几何偏微分方程组,进而给出了单圈自能图、单圈无质量三角图与单双圈真空图在格拉斯曼流形子簇上所有正规奇点邻域的基础解系,从而可以创新性地完成相应费曼积分超几何表达式的解析延拓。
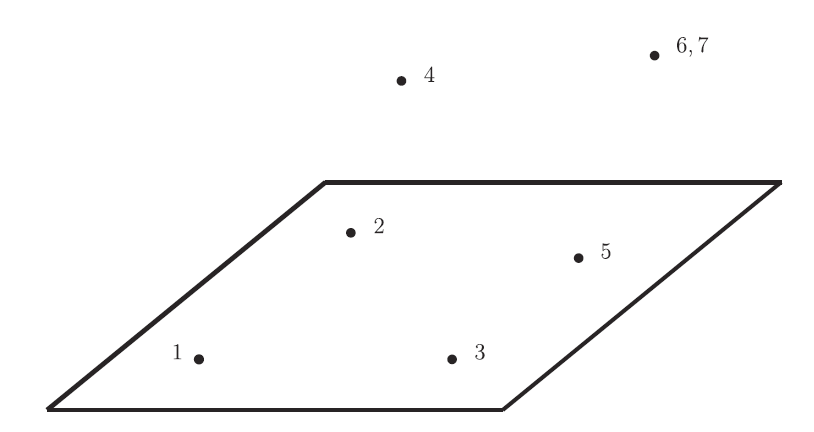
图1费曼积分在格拉斯曼流形子簇上的几何表示图
2、四传播子双圈自能图的GKZ超几何表示
相关工作“GKZ-system of the 2-loop self energy with 4 propagators”发表在《European Physical Journal C》(2023, 83, 314),冯太傅教授为第一兼通讯作者,张海斌副教授为共同通讯作者。
该论文应用Melin-Barnes表示及Miller变换,给出了带质量四传播子的双圈自能图的GKZ超几何偏微分方程组,得到了双圈自能积分的536个超几何解析解,其在非空收敛域下的30个解析解可以组成一个基础解系。值得一提的是,536个解析解形成了200页的排版附在论文的补充材料里。
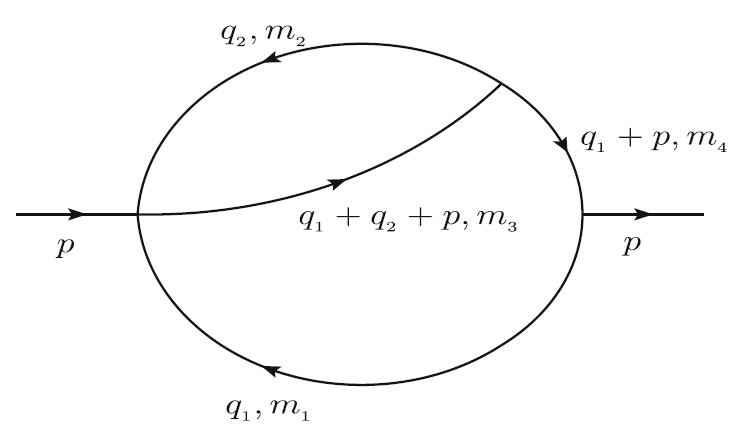
图2四传播子的双圈自能费曼图
3、三圈真空费曼积分的GKZ超几何表示
相关工作“GKZ hypergeometric systems of the three-loop vacuum Feynman integrals”发表在《Journal of High Energy Physics》(2023, 05, 075),张海斌副教授为第一兼通讯作者,冯太傅教授为共同通讯作者。
该论文应用Melin-Barnes表示及Miller变换,给出了带质量的四传播子及五传播子的三圈真空费曼图的GKZ超几何偏微分方程组,得到了在零点及无穷远点邻域上的三圈真空费曼积分的超几何解析解,其在非空收敛域下的解析解可以组成一个基础解系,三圈真空费曼积分可以表示为基础解系的线性组合。
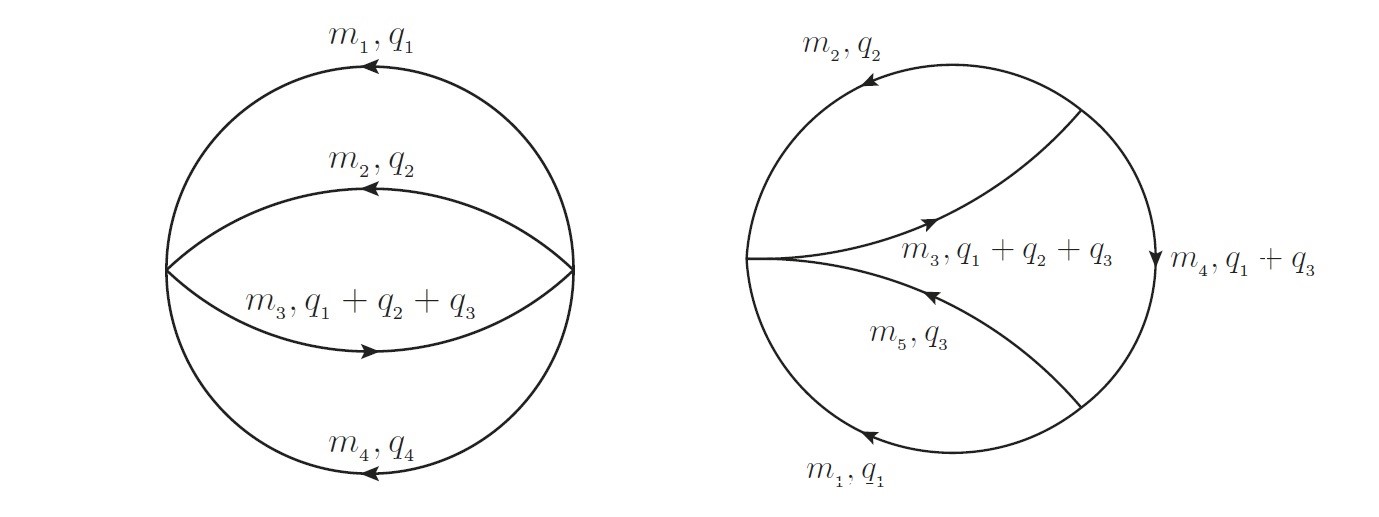
图3四传播子及五传播子的三圈真空费曼图
4、在μν超对称标准模型中考虑单圈修正的上帝粒子稀有衰变h -> MZ
相关工作“Lightest Higgs boson decays h -> MZ in theμfromνsupersymmetric standard model”发表在《Journal of High Energy Physics》, (2023, 05, 134),博士生刘长鑫为第一作者,张海斌副教授与冯太傅教授为共同通讯作者。
该论文在μν超对称标准模型中,计算给出了上帝粒子希格斯玻色子的稀有衰变过程h -> MZ的单圈辐射修正(M为矢量介子ρ,ω,φ, J/ψ,Υ)。数值结果中,详细分析了在μν超对称标准模型中希格斯玻色子的质量及耦合性质,其中右手中微子场对此有重要影响。结合希格斯玻色子及缪子反常磁偶极矩等最新实验数据,给出了在μν超对称标准模型中希格斯玻色子衰变h -> MZ的信号强度,h ->ρZ与h ->ωZ的信号强度可以达到1.2,显示了与标准模型较大的偏离程度,有望在未来的大型粒子对撞机上去探测出来。

图4希格斯玻色子衰变信号强度随参数分布图
上述工作依托于河北省量子场论精细计算与应用重点实验室、河北省计算物理基础学科研究中心等科研平台,得到了国家自然科学基金重点项目、面上项目,河北省杰出青年科学基金项目,河北省青年拔尖人才支持计划项目及yl23455永利yl23455永利公司青年拔尖人才培养项目等经费的资助。
论文链接:
1、https://doi.org/10.1103/PhysRevD.106.116025
2、https://doi.org/10.1140/epjc/s10052-023-11438-6
3、https://doi.org/10.1007/JHEP05(2023)075
4、https://doi.org/10.1007/JHEP05(2023)134

